NCERT Solutions for Class 11 Maths Chapter 15 Statistics

Ex 15.1 Class 11 Maths Question 1.
4, 7, 8, 9, 10, 12, 13, 17
Solution:
Mean of the given data is

Ex 15.1 Class 11 Maths Question 2.
38, 70, 48, 40, 42, 55, 63, 46, 54, 44
Solution:
Mean of the given data is

Ex 15.1 Class 11 Maths Question 3.
13, 17, 16, 14, 11, 13, 10, 16, 11, 18, 12, 17
Solution:
Arranging the data in ascending order, we have
10, 11, 11, 12, 13, 13, 14, 16, 16, 17, 17, 18
Here n = 12 (which is even)
So median is the average of 6th and 7th observations

Ex 15.1 Class 11 Maths Question 4.
36, 72, 46, 42, 60, 45, 53, 46, 51, 49
Solution:
Arranging the data in ascending order, we have 36, 42, 45, 46, 46, 49, 51, 53, 60, 72
Here n = 10 (which is even)
So median is the average of 5th and 6th observations

Find the mean deviation about the mean for the data in Exercises 5 and 6.

Ex 15.1 Class 11 Maths Question 5.

Solution:

Ex 15.1 Class 11 Maths Question 6.

Solution:

Find the mean deviation about the median for the data in Exercises 7 and 8.

Ex 15.1 Class 11 Maths Question 7.

Solution:

Ex 15.1 Class 11 Maths Question 8.

Solution:

Find the mean deviation about the mean for the data in Exercises 9 and 10.

Ex 15.1 Class 11 Maths Question 9.

Solution:

Ex 15.1 Class 11 Maths Question 10.

Solution:

Ex 15.1 Class 11 Maths Question 11.
Find the mean deviation about median for the following data:

Solution:

Ex 15.1 Class 11 Maths Question 12.
Calculate the mean deviation about median age for the age distribution of 100 persons given below:


[Hint: Convert the given data into continuous frequency distribution by subtracting 0.5 from lower limit and adding 0.5 to the upper limit of each class interval]
Solution:

NCERT Solutions for Class 11 Maths Statistics Ex 15.2

Find the mean and variance for each of the data in Exercises 1 to 5.

Ex 15.2 Class 11 Maths Question 1.
6, 7, 10, 12, 13, 4, 8, 12
Solution:
Here xi = 6, 7, 10, 12, 13, 4, 8, 12
∴ Σxi = 6 + 7 + 10 + 12 + 13 + 4 + 8 + 12 = 72
n = 8

Ex 15.2 Class 11 Maths Question 2.
First n natural numbers
Solution:
Here xi = 1, 2, 3, 4, ……….n

Ex 15.2 Class 11 Maths Question 3.
First 10 multiples of 3
Solution:
Here xi = 3, 6, 9, 12, 15, 18, 21, 27, 30,
Σxi = 3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30 = 165
n = 10

Ex 15.2 Class 11 Maths Question 4.

Solution:

Ex 15.2 Class 11 Maths Question 5.

Solution:

Ex 15.2 Class 11 Maths Question 6.
Find the mean and standard deviation using short-cut method

Solution:

Find the mean and variance for the following frequency distributions in Exercises 7 and 8.

Ex 15.2 Class 11 Maths Question 7.

Solution:

Ex 15.2 Class 11 Maths Question 8.

Solution:

Ex 15.2 Class 11 Maths Question 9.
Find the mean, variance and standard deviation using short-cut method.

Solution:

Ex 15.2 Class 11 Maths Question 10.
The diameters of circles (in mm) drawn in a design are given below:

Calculate the standard deviation and mean diameter of the circles.
[Hint: First make the data continuous by making the classes as 32.5 – 36.5, 36.5 – 40.5, 40.5 – 44.5, 44.5 – 48.5, 48.5 – 52.5 and then proceed.]
Solution:

NCERT Solutions for Class 11 Maths Statistics Ex 15.3

Ex 15.3 Class 11 Maths Question 1.
From the data given below state which group is more variable, A or B?

Solution:
For Group A :

Ex 15.3 Class 11 Maths Question 2.
From the prices of shares X and Y below, find out which is more stable in value:

Solution:

Ex 15.3 Class 11 Maths Question 3.
An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:

(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm, AorB, shows greater variability in individual wages?
Solution:
(i) Firm A :
Number of wage earners (n1) = 586
Mean of monthly wages (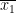) = Rs.5253
∴ Total monthly wages = 5253 x 586
= Rs. 3078258
Firm B :
Number of wage earners (n2) = 648
Mean of monthly wages () = Rs.5253
∴ Total monthly wages = 5253 x 648
= Rs. 3403944
Hence, Firm B pays larger amount as monthly wages.

(ii) Since both the firms have same mean of monthly wages, so the firm with greater variance will have more variability in individual wages. Thus firm B will have more variability in individual wages.

Ex 15.3 Class 11 Maths Question 4.
The following is the record of goals scored by team A in a football session:

For the team B, mean number of goals scored per match was 2 with a standard deviation 1.25 goals. Find which team may be considered more consistent?
Solution:
For team A:

Ex 15.3 Class 11 Maths Question 5.
The sum and sum of squares corresponding to length x (in cm) and weight y (in gm) of 50 plant products are given below:

Which is more varying, the length or weight?
Solution:

Class 11 Maths NCERT Solutions  – Miscellaneous Questions

Miscellaneous Exercise Class 11 Maths Question 1:

Ans:

Ex 15.3 Class 11 Maths Question 2:

Ans:

Ex 15.3 Class 11 Maths Question 3:

Ans:

Ex 15.3 Class 11 Maths Question 4:

Ans:

Ex 15.3 Class 11 Maths Question 5:

Ans:

Ex 15.3 Class 11 Maths Question 6:

Ans:

Ex 15.3 Class 11 Maths Question 7:

Ans:

Exercise 15.1

Q1. Calculate the mean deviation about the mean for the given data

5, 8, 9, 10, 11, 13, 14, 18

Q2. Calculate the mean deviation about the mean for the given data

39, 71, 49, 41, 43, 56, 64, 47, 55, 45

Q3. Calculate the mean deviation about the median for the given data:

13, 16, 11, 10, 11, 12, 17, 14, 13, 16, 18, 17

Q4. Calculate the mean deviation about the median for the given data:

36, 46, 60, 53, 51, 72, 42, 45, 46, 49

Q5. Calculate the mean deviation about the mean for the given data

xi	5	10	15	20	25
fi	7	4	6	3	5

Q6. Calculate the mean deviation about the mean for the given data

xi	10	10	15	20	25
fi	7	4	6	3	5

Q7. Calculate the mean deviation about the median for the given data

xi	10	10	15	20	25
fi	7	4	6	3	5

xi	5	7	9	10	12	15
fi	8	6	2	2	2	6

Q8. Calculate the mean deviation about the median for the given data

xi	15	21	27	30	35
fi	3	5	6	7	8

Q9. Calculate the mean deviation about the mean for the given data:

Income per day	Number of persons
0 – 100	4
100 – 200	8
200 – 300	9
300 – 400	10
400 – 500	7
500 – 600	5
600 – 700	4
700 – 800	3

Q10. Calculate the mean deviation about the mean for the given data:

Height in cm	Number of boys
95 – 105	9
105 – 115	13
115 – 125	26
125 – 135	30
135 – 145	12
145 – 155	10

Q11. Calculate the mean deviation about the median for the given data:

Marks	Number of girls
0 – 10	6
10 – 20	8
20 – 30	14
30 – 40	16
40 – 50	4
50 – 60	2

Q12.  Calculate the mean deviation about the median for the given data:

            

Age	Number
16 – 20	5
21 – 25	6
26 – 30	12
31 – 35	14
36 – 40	26
41 – 45	12
46 – 50	16
51 – 55	9

Exercise 15.2

Q1. Calculate mean and variance for the given data 6, 7, 10, 12, 13, 4, 8, 12

Q2. Calculate the mean and variance for the first n natural numbers.

Q3. Calculate the mean and variance for the first 10 multiples of 3.

Q4. Calculate the mean and variance for the data

xi	6	10	14	18	24	28	30
fi	2	4	7	12	8	4	3

Q5. Calculate the mean and variance for the data

xi	92	93	97	98	102	104	109
fi	3	2	3	2	6	3	3

Q6. Calculate the mean and standard deviation using short-cut method.

xi	60	61	62	63	64	65	66	67	68
fi	2	1	12	29	25	12	10	4	5

Q7. Calculate the mean and variance for the given frequency distribution.

Classes	0 – 30	30 – 60	60 – 90	90 – 120	120 – 150	150 – 180	180 – 210
Frequencies	2	3	5	10	3	5	2

Q8. Calculate the mean and variance for the following frequency distribution.

Classes	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
Frequencies	5	8	15	16	6

Q9. Calculate the mean, variance and standard deviation using short – cut method:

Height in cm	Number of children
70 – 75	3
75 – 80	4
80 – 85	7
85 – 90	7
90 – 95	15
95 – 100	9
100 – 105	6
105 – 110	6
110 – 115	3

Q10. The diameters of circles (in mm) drawn in a design are given below:

Diameters	Number of Children
33 – 36	15
37 – 40	17
41 – 44	21
45 – 48	22
49 – 52	25

Exercise 15.3

Q1. From the data given below state which group is more variable, A or B 

Marks	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	70 – 80
Group A	9	17	32	33	40	10	9
Group B	10	20	30	25	43	15	7

Q2. From the prices of shares X and Y below, find out which is more stable in value.

X	35	54	52	53	56	58	52	50	51	49
Y	108	107	105	105	106	107	104	103	104	101

Q3. An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:

	Firm A	Firm B
No. of wage earners	586	648
Mean of monthly wages	Rs. 5253	Rs. 5253
Variance of the distribution of wages	100	121

(i) Which firm A or B pays larger amount as monthly wages?

(ii) Which firm, A or B, shows greater variability in individual wages?

Q4. The following is the record of goals scored by team A in a football session:

Number of goals scored	0	1	2	3	4
Number of matches	1	9	7	5	3

For the team B, mean number of goals scored per match was 2 with standard deviation 1.25 goals. Find which team may be considered more consistent?